Hello Alan,
As you remember from our discussion ~10 years ago during my Phd, Molflow is an event-driven simulator only aware of physics on the walls. It has no test cubes or other volume-aware features (even though we plan to add for custom parameters for the background scattering).
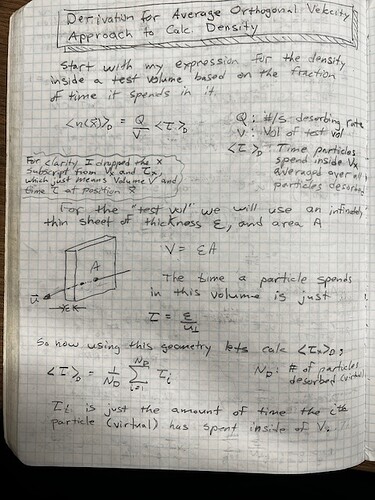
Instead of saying “it’s impossible to measure density”, I made a best-effort approach to estimate the density, that works most - but not all - of the time.
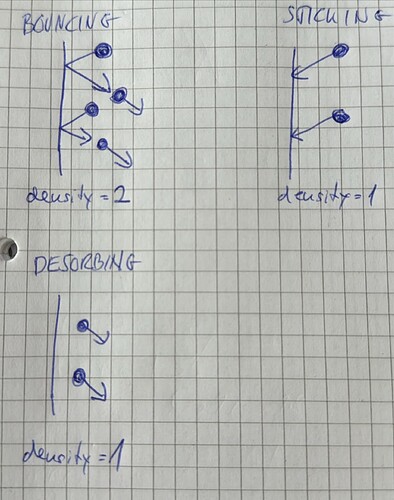
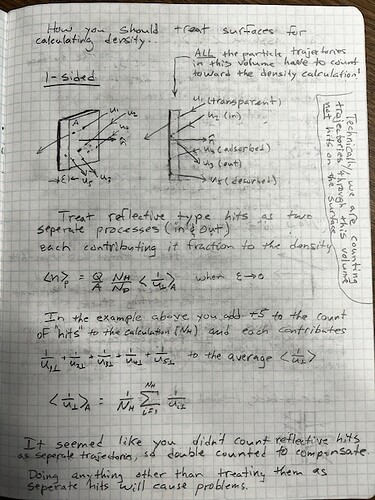
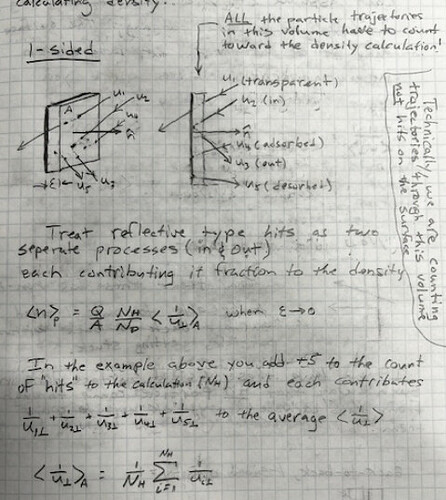
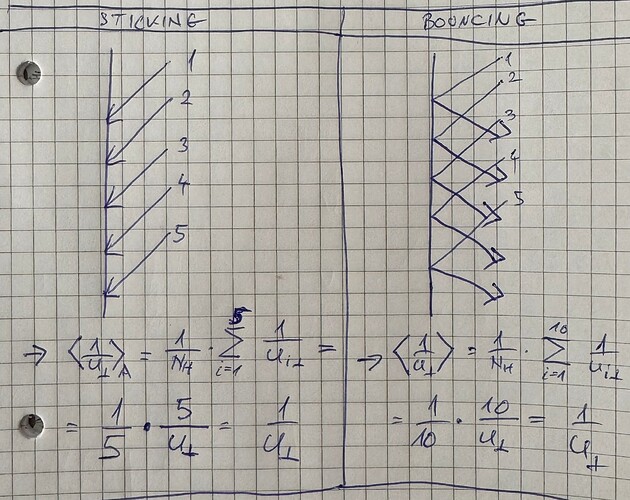
Look at the three cases above. It’s obvious that when sticking=1 or desorption is 100%, the density is half of the bouncing case. The problem is, Molflow can only detect incident hits on the wall, so in all three cases it would measure the same density!
Therefore, I added a correction factor, I paste the code below, it’s enough if you read my comments:
/**
* \brief Function that calculates a density correction factor [0..1] (with 1.0 = no correction)
* \return correction factor value [0..1]
*/
double InterfaceFacet::DensityCorrection() {
//Correction for double-density effect (measuring density on desorbing/absorbing facets):
//Normally a facet only sees half of the particles (those moving towards it). So it multiplies the "seen" density by two.
//However, in case of desorption or sticking, the real density is not twice the "seen" density, but a bit less, therefore this reduction factor
//If only desorption, or only absorption, the correction factor is 0.5, if no des/abs, it's 1.0, and in between, see below
if (facetHitCache.nbMCHit > 0 || facetHitCache.nbDesorbed > 0) {
if (facetHitCache.nbAbsEquiv > 0.0 || facetHitCache.nbDesorbed > 0) {//otherwise save calculation time
return 1.0 - (facetHitCache.nbAbsEquiv + (double)facetHitCache.nbDesorbed) / (facetHitCache.nbHitEquiv + (double)facetHitCache.nbDesorbed) / 2.0;
}
else return 1.0;
}
else return 1.0;
}
This works in practically all the cases, except when you “fool” Molflow, or in other words, you make it impossible to deduce the real density. Let’s walk through your geometry:
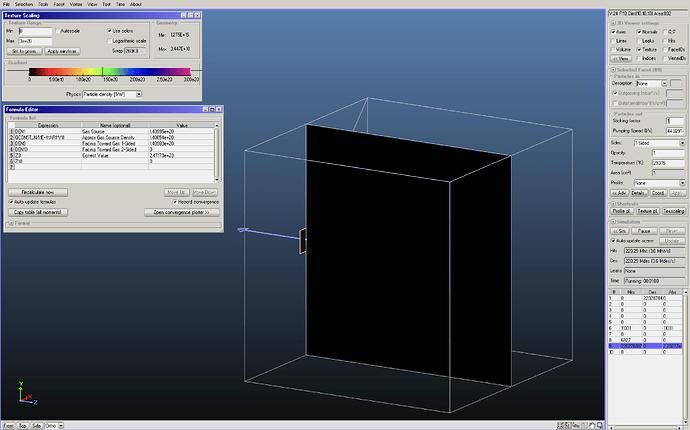
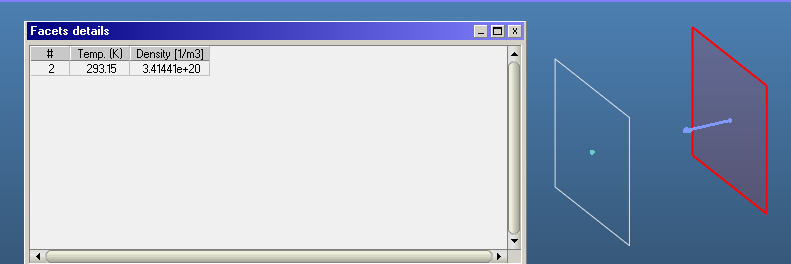
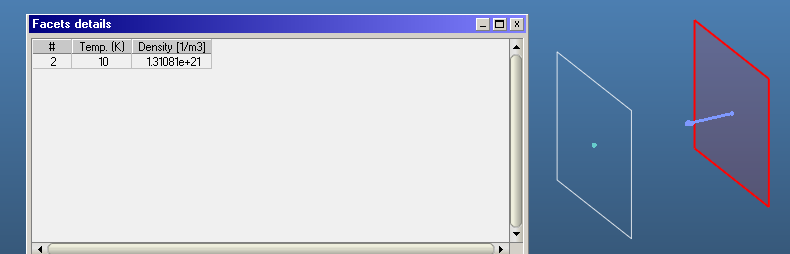
- Your desorbing facet, leftmost in your screenshot, counts only desorptions. Therefore Molflow uses a correction factor of 0.5 because it knows that particles are not coming in, only going out.
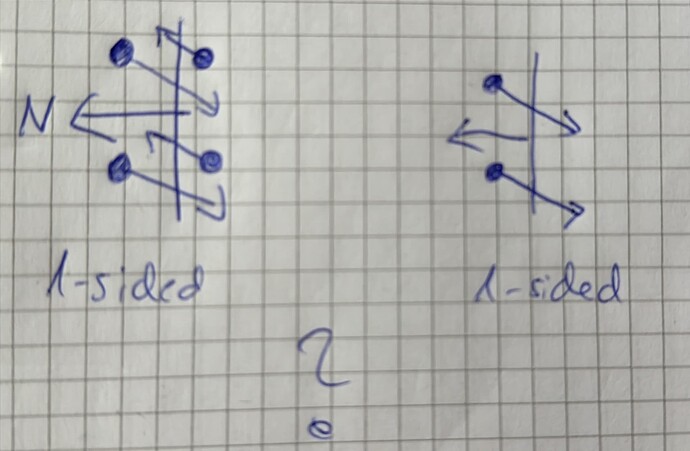
- Your next facet, looking left, transparent, cannot apply a correction factor because it doesn’t know what’s going on behind it. Look at the two cases, it cannot decide which is going on, so it assumes that particles are coming from its back, it just can’t detect them:
(you and me, of course, know that it’s the right-side case, but most MolFlow geometries are isotropic, so the left, general case is the safer assumption)
Therefore it overestimates the density by a factor of 2. When you switch to 2-sided, it correctly detects that there are no particles coming from the back, and shows the correct density (half of the 1-sided version)
- Your last facet, pointing away from the source can’t detect any hit so it - incorrectly - shows 0 density.
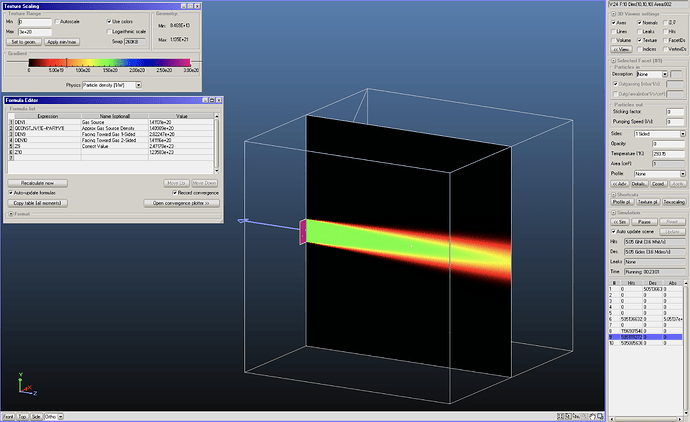
Just to be clear, as you know as well, density is a scalar, it shouldn’t be affected by the facet’s orientation. As you can see, even in your jet geometry, Molflow calculates the density well, despite very different number of hits, regardless of orientation, if you “help” it by giving information from both sides:
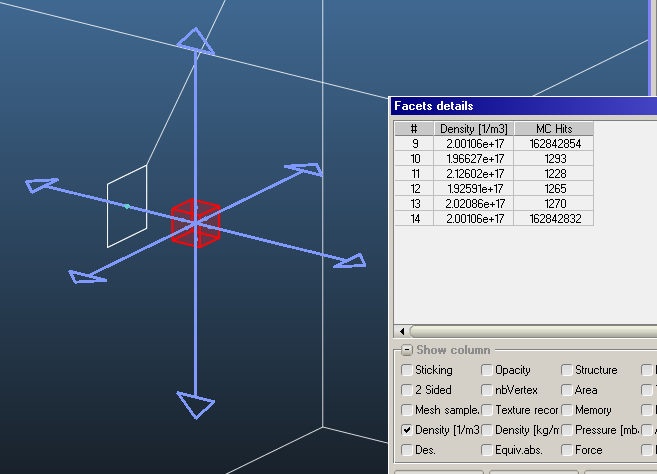
(These are transparent two-sided facets. 9 and 14 are perpendicular to the jets, 10-13 are parallel).
But please understand that 1-sided facets are usually located as the wall of the geometry, and it would be unacceptable to average the 0-density on the outer side of the geometry and the actual density, nor would it be acceptable to double the estimated density in the volume just because the facet is 1-sided.
Conclusion:
- I can’t measure the density directly, so I implemented a best-effort estimation
- Even in non-isotropic systems, this shows correct density, but transparent facets need to be 2-sided
- 1-sided transparent facets in a non-isotropic system are an edge case where I believe there’s not enough information to correctly show the density, only to assume isotropy, which in your case overestimated the density
Final note:
- 2-sided facets aren’t that mythical - they simply detect hits from both sides, and in any formula where there is normalization by facet area, they double the facet area (pressure, impingement, density). Apart from double-counting the area, I don’t do further magic or corrections on them.