Hello all,
Although Molflow+ is an attractive software for vacuum system simulations, I am concerned about the validity of the outputs. I tried to evaluate the conductance between the main chamber and the pumping station in my system using Molflow+. Moreover, I simulated the pressure distribution in the chamber to evaluate the pressure difference between different parts of the system. How can I ensure the validity of these results?
Thank you
Dear Marton,
Thank you for your response.
Do you have any information about the error in the simulation outputs? For example, suppose I have simulated a vacuum chamber and used Molflow to calculate the particle density in a specific region of the chamber. Do you know the percentage error of the results obtained, assuming that I have accurately entered the system parameters such as geometry, pumping speed, and outgassing?
For the detailed reply, see section 1.2.1.9 on page 23 of my thesis.
Since I wrote the thesis there’s a new tool called convergence plotter to see the percentage value in an actual simulation, in your example you’d create a formula for the density first, for example DEN123 is the density on facet 123.
The transmission probability calculation has an associate standard deviation (binomial distribution) given by an analytical formula: if p is the transmission probability, then the “true value” will be contained in the band given by
P_tr = p +/- (sqrt(1-p)*p/N_tr)
where N_tr is the number of TRANSMITTED molecules.
So, if you have P_tr=50% you need to have N_tr=2500 in order to have sigma=1%.
Sigma goes with the square of N_tr, so to reduce sigma by a factor of 10 you need to run 100x longer the simulation. This is why TPMC is sometimes avoided and alternate methods are used. If your p is very small, i.e. N_tr/Ntot is small, you’d need to run the simulation for a very long time, or use a powerful computer. In literature you can find people who do that routinely, like those at KIT in Karlsruhe, on their ProVac3D code (similar to Molflow+) which has been adapted to run on GPU-based parallel supercomputers ("Marconi, in Italy).
Therefore, for a given geometry, and therefore p value, you can calculate how many N_tr molecules you’ll need to generate before you reach a statistical error of x%, by reversing the formula above.
More details for instance in this excellent paper:
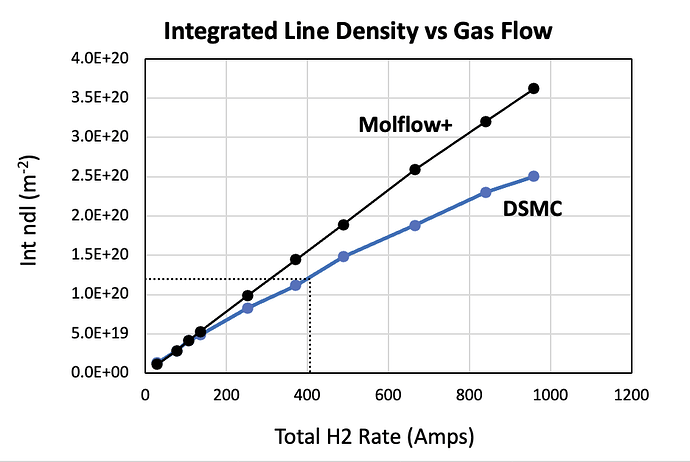
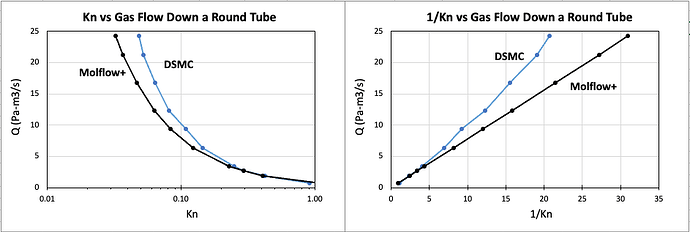
I have personally validated tens of calculations/measurements found in literature, when sufficient details had been made available that allowed me to make a Molflow+ model of the system discussed in the articles, and I have always found a very good, if not perfect, agreement with those data. The only deviations start to be visible when the mean-free path comes close to the Knudsen regime, also called transitional regime, the one that connect the free-molecular flow region to the viscous flow one. I have shown some examples throughout the years on various occasions, mainly workshop and conference presentations… unfortunately I do not have now the time to link them here, sorry.
Summary: based on decades of use of the code, you can safely assume that its output is correct. This means, though, that the geometrical model you built and the physical assumptions/properties you assigned to it are a faithful representation of the real physical model.
