Hi there!
I am trying to model a vacuum system featuring several domains
Hello Pierlugi,
I’ll discuss this with @rkerseva and get back to you, interesting problem.
Regards, Marton
Hello again,
It is not straightforward
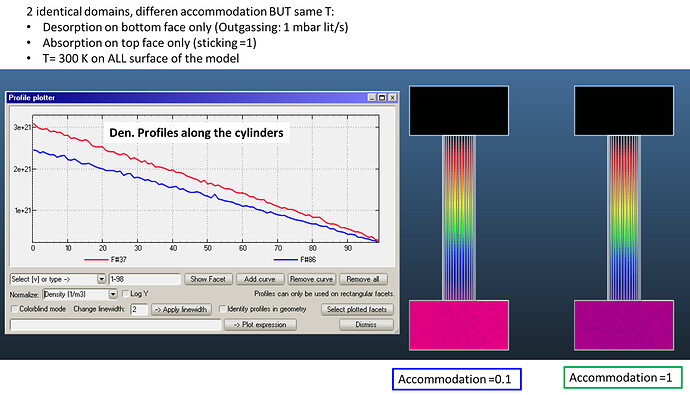
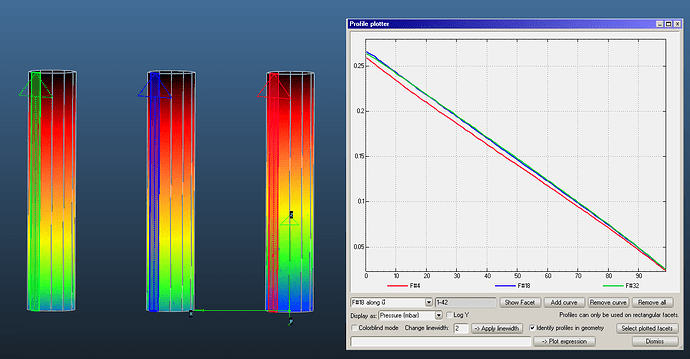
I have created three pipes with accomodation coefficients 1, 0.5 and 0.1.
You can see that the pressure is slightly larger for the low accomodation pipes:
This is due to a different velocity distribution:
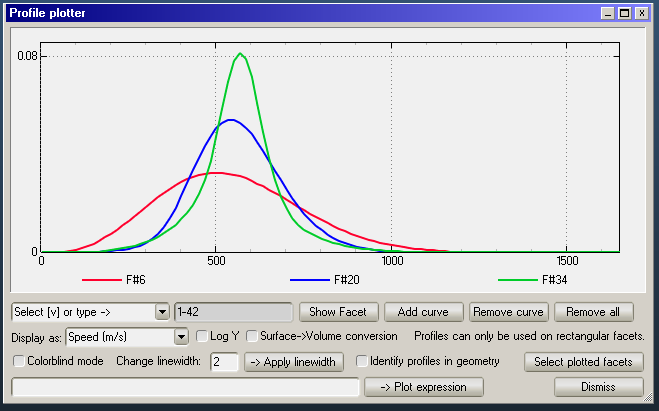
Low accomodation coefficient tubes have slightly faster molecules. The reason is that accomodation coefficient is defined in terms of energy, not speed:
New_energy = old_energy+(wall_energy-old_energy)*accomodation_coefficient
in simple terms, acc=1 will alwas assign “wall energy” (Maxwell-Boltzmann distribution according to wall temperature), acc=0 will keep old molecule speed, and acc=0.5 will take the average energy between old and wall.
Because of this, since E~v^2, the averaging tends to increase molecule speed. In plain simple English, fast moelcules lose speed more difficultly than slow molecules gain speed.
If you bear with me, a concrete numerical example for 4 molecules in a box, accomodation=50%.
In the beginning, the average speed is 2m/s, and for simplicity let’s assume E=v^2.
The molecules follow a dead simple velocity distribution: half of them are 1m/s and half 3m/s.
Initial speeds: 1m/s 1m/s 3m/s 3m/s (avg=2ms)
Inital energies: 1J 1J 9J 9J (avg=5J)
First collision:
old energies: 1J 1J 9J 9J (avg 5J)
new “wall” energies: 1J 9J 1J 9J (avg 5J)
thermalized energies after collision: 1J 5J 5J 9J (avg 5J)
thermalized speeds after collision ( sqrt(5)=2.236 ): 1m/s 2.236m/s 2.236m/s 3m/s (avg 2.118m/s)
As you can see even if the wall had the same distribution ans the initial, the collision shifted the velocity from 2m/s to 2.118m/s
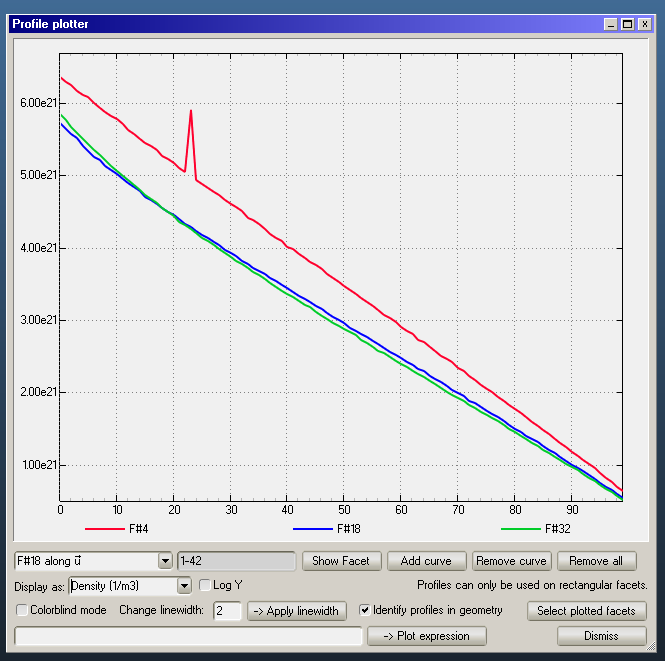
In case of density, the relation is the inverse of the pressure: slower molecules are more dense:
I will discuss with Roberto whether apart from the current accomodation definition (in terms of energy) we should introduce a new one (in terms of speed). This would require a bit of literature reading to see concrete examples of partial thermalization. If you let us know what you’re trying to simulate, maybe we can give advice for the best approach.
Hope I was clear, and thanks for bringing up the issue, Marton
Thank you Marton for prompt and very detailed answer. In fact it was not straightforward…
My application is to model the vacuum system of a “neutral beam injector”, an high power beamline used in nuclear fusion context. I am sure that Roberto knows what I am talking about 
The system is characterized by a large vessels containing some “boxes” that the beam has to cross.
These are characterized by very different pressure: one box is a gas cell (see for example: here
) to convert the ions into neutrals, and because of heating by the beam itself some part of the beamline can have T op to 100 C, while other part are at ambient temperature.
In principle the standard approach of Molflow for non isothermal system should work I think, do you agree?
thanks again for your help.
Hello Pierluigi, and thanks for sharing some info about your project, appreciated.
NBIs are huge beasts, with typically large cryopanels over a long and wide area (along the beam path). Just make sure you look at the particle density rather than the pressure, because the latter is direction-dependent in molecular flow, while density is not, it’s a scalar. This is especially true when large sticking coefficient are involved, which is often the case with NBIs’ cryopanels.
Last year, a similar application has used Molflow, for one of the chinese tokamaks… the paper is in the “Results” section of our web site… Results - MolFlow+ / SynRad+ documentation (cern.ch) , the title is “Vacuum System Optimization for EAST Neutral Beam Injector”.
Cheers, and don’t hesitate to contact us again in case of need (or simply to share your results).
Thanks Roberto for this additional advices! I am progressing in the model and hope to conclude soon. I have another question that I will maybe post separately in the forum (slightly different topic) and a proposal of additional “tool” for molflow (use of “parameters”), that I will also write in appropriate part of forum. Thank you both to have made Molflow available and to keep the project active!
